Hinweise zur Fehlerrechnung
Die folgenden Punkte sind keine vollständige Skripte zur Fehlerrechnung, sondern einfach eine Liste von wichtigen Punkten, wegen deren Nichtbeachtung in Laborberichten/Protokollen häufig "der Wurm drin ist".(0) Was ist Fehlerrechnung?
Fehlerrechnung ist die quantitative Ermittlung der Ungenauigkeit der Messdaten sowie der aus den Messdaten ermittelten Größen. Fehlerrechnung hat NICHTS mit einem Vergleich der eigenen Ergebnisse mit Literaturwerten zu tun. Fehlerrechnung bezieht sich ausschließlich auf eine Analyse der eigenen Daten.(1) Signifikante Stellen
- Signifikante Stellen in einer Maßzahl sind diejenigen Stellen, die sich aus Messdaten experimentell unter Berücksichtigung des Messfehlers ergeben und nicht bloß der Angabe der Größenordnung dienen.
- Wenn Stellen in einer Zahl nur der Angabe der Größenordnung dienen, dürfen nur Nullen verwendet werden.
- Ganzzahlen ("integers", Zahlen „ohne Komma“):
- Signifikante Stellen = Zahl der Ziffern ohne nachfolgende Nullen. Beispiele:
- 1230 → 3 sign. Stellen
- 1230000 → 3 sign. Stellen
- 123 → 3 sign. Stellen
- Nullen dienen nur zur Angabe der Zehnerpotenzen, sind nicht signifikant!
- Gleitkommazahlen (Zahlen „mit Komma“, "floating point"):
Nullen am Ende sind signifikant, Beispiel:
- 1,23 → 3 sign. Stellen
- 1,230 → 4 sign. Stellen
(2) Signifikante Stellen bei Angabe von Größe und Fehler
- Die Angabe "4,3 V" impliziert bereits einen maximalen Fehler von ±0,05 wegen der Rundung.
- Wert und Fehlerangabe müssen hinsichtlich der signifikanten Stellen zueinander passen. Folgendes geht gar nicht (Beispiel Faraday-Konstante F):
- F = (96432,2315 ±2137,34) C/mol. ← Total falsch!! weil:
- Wenn ΔF ≈2000 C/mol , darf auch nur die Tausenderstelle des Wertes als letzte signifikante Stelle angegeben werden.
- So genau wie hier angegeben ist der Fehler nicht bekannt.
- F = (96000 ±2000) C/mol. So ist es richtig, weil:
- Vom Wert sind nur die Tausender bekannt, also nur 2 signifikante Stellen, der Rest wird mit Nullen aufgefüllt.
- Vom Fehler kennen wir nicht den Fehler (den Fehler 2. Ordnung), deshalb geben wir beim Fehler nur 1 signifikante Stelle an.
- Ausnahme: wir dürfen die 2. Stelle des Fehlers auch auf die "5" runden, also:
- ΔF = 2120 C/mol → ΔF = 2000 C/mol
- ΔF = 2470 C/mol → ΔF = 2500 C/mol
- ΔF = 2820 C/mol → ΔF = 3000 C/mol
- Wir haben also die erste Stelle des Fehlers gezehntelt (alle Ziffern erlaubt von 0..9) und die zweite Stelle nur noch gehälftelt (nur 0 und 5 erlaubt). Das ist desweben erlaubt, weil sonst der Unterschied zwischen maximalem Fehler und wahrscheinlichstem Fehler verschwindet.
- Beim Fehler wird kaufmännisch gerundet, es wird nicht einfach aufgerundet. Man würde sonst die Absurdität erzeugen, dass aus dem Rohwert ΔF = 2010 C/mol der Fehler ΔF = 3000 C/mol wird, aber aus dem Fehler ΔF = 1990 C/mol ergäbe sich der Fehler ΔF = 2000 C/mol. Eine Mini-Änderung ergäbe eine gigantische Schlechtrechnung der Messung. Das macht nicht viel Sinn.
(3) Fehlerfortpflanzung
Ergibt sich eine Größe G multiplikativ aus drei Größen X, Y und Z wie folgt:G = X × Y / Z,
dann ist der maximale relative Fehler von G gleich der Summe der relativen Fehler der Größen X, Y und Z:
δGmax = δX + δY + δZ.
Dabei spielt es keine Rolle, ob eine der Größen im Zähler oder im Nenner steht.
Man hat zu unterscheiden zwischen dem maximalen und dem wahrscheinlichsten Fehler:
Die Größe G ergebe sich aus 2 Größen X und Y wie folgt:
G = X × Y
Dann gilt für den relativen Fehler δGmax:
δGmax = δX + δY.
Die beiden (orthogonalen) Vektoren im Fehlerraum wurden hier algebraisch addiert.
Wir können die Vektoren aber auch vektoriell addieren und erhalten dann den wahrscheinlichsten Fehler (Pythagoras):
(δG)2 = (δX)2 + (δY)2.
und somit
δG = √ (δX)2+ (δY)2) .
Diese Art der Quadrataddition kann auch verwendet werden, wenn mehr als 2 fehlerbehaftete Größen auftreten.
Ist δX = δY = 0.01,
so ist
δGmax = 0.02 = 2%
und
δG = √2 × 0.01 = 0.014142...
Um diesen Unterschied mitzunehmen, erlauben wir der 2. Stelle die Rundung auf die "5" (siehe oben) und geben den Fehler wie folgt an:
δG = 0.015 = 1,5%.
(4) Ausgleichsgeraden: da kann man viel falsch machen...
Ausgleichsgeraden werden im PC-Praktikum normalerweise mittels Datenanalyse-Software bestimmt (empfohlen ist Igor Pro). Unter Umständen ist aber der funktionelle Zusammenhang nicht im gesamten Messbereich linear, sondern nur in einem bestimmten Bereich. Dies ist in der nachfolgenden Abbildung gezeigt: die ersten beiden Datenpunkte im x-Bereich 0..2 liegen offensichtlich nicht auf der Geraden, die den Wertebereich x=2..9 beschreibt.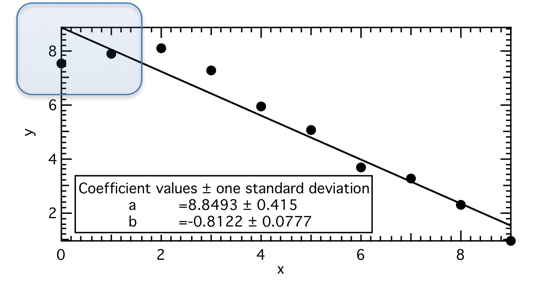
Daher liefert auch die Anpassungsgerade schlechte Resultate.
Wenn man die beiden ersten Punkte bei der Ausgleichsgerade nicht "mitnimmt", ergibt sich eine viel bessere Ausgleichsgerade:
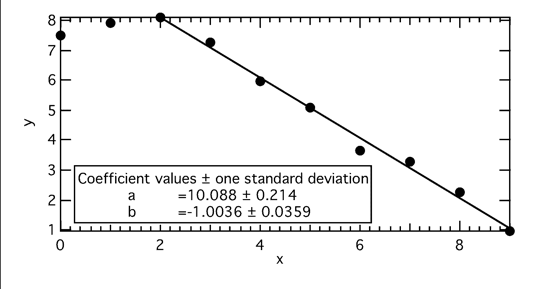
Den in die Graphik eingetragenen Werten für Steigung und Achsabschnitt können Sie entnehmen, dass die Standardabweichung für den zweiten Fall deutlich kleiner wird. Maskieren Sie bei Ausgleichsgeraden offensichtlich falsche Bereiche!
18.11.2012, RF
