
Physikalisch-Chemische Praktika
Bestimmung des Diffusionskoeffizienten von Isopentan in Luft bei einer Temperatur von 26\(^0\)C.
Wie schnell verdampft eine Flüssigkeit? Nach wie langer Zeit ist eine wassergefüllte Schale durch Verdampfung leer?
Ob eine Flüssigkeit überhaupt verdampft, hängt zunächst vom effektiven Dampfdruck \(p^{D}_{\rm eff}\) ab; dieser ist gleich der Differenz aus dem Gleichgewichtsdampfdruck bei der gegebenen Temperatur und der Partialdruck des Dampfes in der Gasphase oberhalb der Flüssigkeit. Bei Wasser wird dies als Feuchte bezeichnet; ist die relative Feuchte gleich 100%, so findet überhaupt keine Netto-Verdampfung statt; der Flüssigkeitsspiegel ändert sich nicht.
Unmittelbar oberhalb der Flüssigkeitsoberfläche ist der Partialdruck des Dampfes stets gleich dem Gleichgewichtsdampfdruck; daher würde eine Flüssigkeit überhaupt nicht verdampfen, wenn nicht ein Abtransport des Dampfes von der Flüssigkeitsoberfläche weg erfolgen würde.
Der Abtransport kann auf zwei verschiedenen Mechanismen beruhen:
Wir sind hier am diffusiven Stofftransport interessiert. Die Grundlagen der molekularen Diffusion durch eine Fläche \(A\) wird u.a. durch das 1. Ficksche Gesetz beschrieben: \begin{equation} \label{eqFick1} J = \frac{1}{A} \frac{\diff n}{\diff t} = - D \frac{\diff c}{\diff z}. \end{equation}
\(J:\) Stofftransport (Fluss) in der Einheit \({\rm \frac{mol}{s \cdot m^{2}}}\);
\(A\): Fläche, durch die der Stofftransport erfolgt in der Einheit \({\rm m^{2}}\);
\(n\): Stoffmenge in der Einheit \({\rm mol}\);
\(t\): Zeit in der Einheit \({\rm s}\);
\(c\): Konzentration in der Einheit \({\rm mol/m^{3}}\);
\(z\): Diffusionsrichtung in der Einheit \({\rm m}\);
\(D\): Diffusionskoeffizient in der Einheit \({\rm \frac{m^{2}}{s}}\).
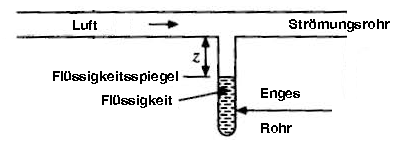
Zur Bestimmung des Diffusionskoeffizienten von Isopentan in Luft wird ein Stefan-Rohr genutzt. Der prinzipielle Aufbau ist in der Abb. 1 gezeigt.

Das Stefan-Rohr ist im einfachsten Fall ein thermostatisiertes Strömungsrohr, an das senkrecht ein kleines Glasröhrchen angebracht ist, in dem sich eine Flüssigkeit befindet. Durch das Strömungsrohr strömt fortwährend ein Gas, im einfachsten Fall Luft. Das Volumen oberhalb des Röhrchens (innerhalb des Strömungsrohrs) ist somit stets frei von Dampf aus der Flüssigkeit, weil diese vom Luftstrom wegtransportiert wird. Der Partialdruck des Dampfes unmittelbar oberhalb der Flüssigkeit ist gleich \(p^{D}\), und am Eintrittsort in das Strömungsrohr ist \(p_{i}=0\).
Es liegt also längs der Strecke \(\Delta z\) ein Partialdruck-Abfall \(\Delta p_{i}\) vor.
Würde sich die Höhe des Flüssigkeitsspiegels durch die Verdampfung nicht ändern (indem man beispielsweise verdampfte Flüssigkeit nachfüllen würde) , so wäre der Konzentrationsgradient \(\frac{dc}{dz}\) bzw. der Partialdruckgradient \(\frac{1}{RT}\frac{dp}{dz}\) in jeder beliebigen Position \(z\) zwischen dem Flüssig"-keits"-spiegel und der Eintrittsstelle in das Rohr konstant. Gemäß dem 1. Fickschen Gesetz wäre damit auch der Fluss \(J\) konstant. Würde man also unter diesen Bedingungen die im Luftstrom abtransportierte Stoffmenge ausfrieren und wägen, so könnte man den Diffusionskoeffizienten unmittelbar bestimmen.
Da aber der Flüssigkeitsspiegel durch das Verdampfen abnimmt und der Dampf im Strömungsrohr abtransportiert wird, wird \(\Delta z\) im Laufe der Zeit größer, während \(\Delta p_{i}\) längs \(\Delta z\) immer gleich bleibt. Daher wird \(\frac{\Delta p_{i}}{\Delta z}\) allmählich kleiner (bitte beachten Sie: er wird deswegen kleiner, weil \(\Delta z\), also der Nenner des Bruchs, größer wird!)
Die Herleitung der Änderung des Füllstandes als Funktion der Zeit ist im Anhang wiedergegeben. Die Herleitung folgt der Darstellung in Ref. [1]. Man gelangt zu folgender Gleichung für den Diffusionskoeffizienten:
Mit \[ k = \frac{RT \varrho_{A}}{2 p^0 M_{A}} \] findet man: \begin{equation} \label{eqStefan1} D_{AB} = - k \cdot \frac{z^{2} - z_{0}^{2} }{t} \cdot \left[{\ln\left(1 - \frac{p^{D}}{p^{0}} \right)}\right]^{-1} \end{equation}
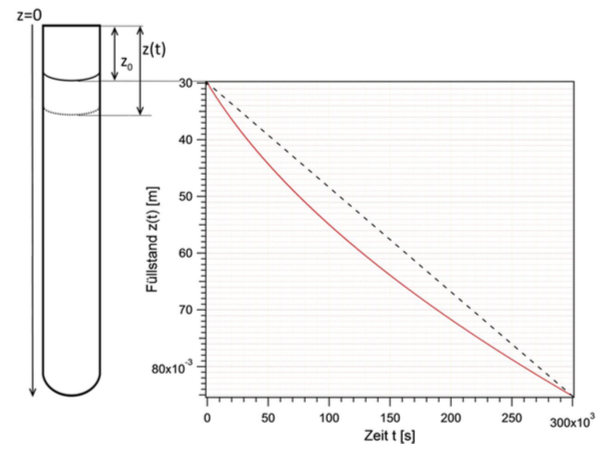
Bitte beachten Sie, dass zwischen den Variablen \(z\) und \(t\) kein linearer Zusammenhang besteht. Die Verdampfung erfolgt also nicht gleichförmig, sondern verlangsamt sich mit sinkendem Flüssigkeitsspiegel allmählich.
Fassen wir die Konstante \(k\) und den ebenfalls konstanten Ausdruck \( \left[{\ln\left(1 - \frac{p^{D}}{p^{0}} \right)}\right]^{-1} \) zu einer neuen Konstanten \(K\) zusammen, so erhalten wir aus Gl. \ref{eqStefan1}:
Vorzeichenbetrachtung: Da \(1 - \frac{p^{D}}{p^{0}} < 1\), ist der Logarithmus in Gl. \ref{eqStefan1} negativ; daher ist auch \(K\) negativ. \(z\) nimmt also mit steigender Zeit zu, wie es auch zu erwarten ist für den Abstand des Meniskus vom Eintrittsort in das Strömungsrohr.
Die Position der Flüssigkeitsoberfläche hängt also von der Wurzel aus der verstrichenen Zeit ab. Die Nicht-Linearität ist von umso größerer Bedeutung, je mehr der Meniskus abnimmt (vgl. Abb. \ref{eqStefan2}).
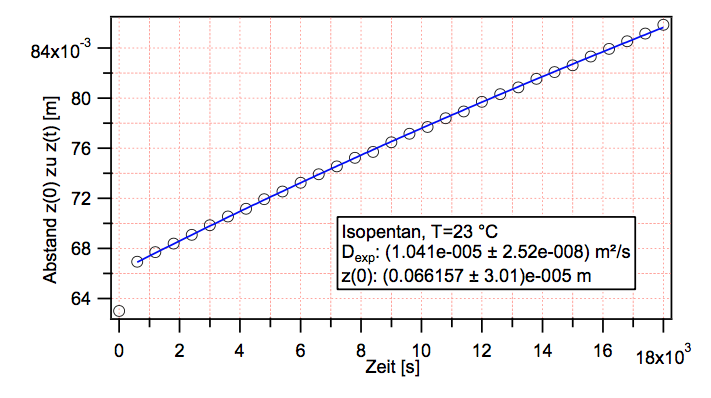
Die Gl. \ref{eqAuswertung} erlaubt es, den Diffusionskoeffizienten \(D_{AB}\) einer Substanz in einer Substanz B zubestimmen. Man bestimmt für verschiedene Zeiten aus dem Flüssigkeitsstand jeweils durch Anwendung der Gl. \ref{eqAuswertung} den Diffusionskoeffizienten \(D_{AB}\) (der Literaturwert des Diffusionskoeffizienten von Isopentan in Luft beträgt bei 26\(^0\)C: \(D=7,92 \cdot 10^{-6} \; {\rm m^2/s}\) [3]). Misst man den Füllstand zu verschiedenen Zeiten, so kann man bzgl. \(D_{AB}\) einen Mittelwert, eine Standardabweichung und einen Fehler des Mittelwertes berechnen. Die Berechnungen lassen sich bequem mit Hilfe des Programmes "Microsoft Excel" durchführen.

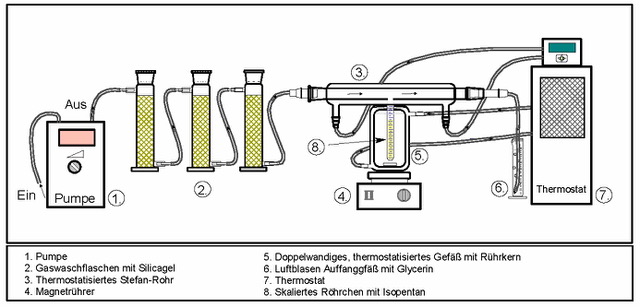
Typische Messergebisse für Isopentan sind in der Abb. 5 gezeigt
| Symbol | Einheit | |
|---|---|---|
| \(u_{i}\) | Durchschnittsgeschwindigkeit der Komponente \(i\) bzgl. eines stationären Beobachters | \({\rm \frac{m}{s}}\) |
| \(u\) | Massengeschwindigkeit | \({\rm \frac{m}{s}}\) |
| \(U\) | Molare Geschwindigkeit; \(U = \frac{1}{c} \cdot \sum_{i=1}^{n} c_{i} u_{i}\) | \({\rm \frac{m}{s}}\) |
| \(n_{i}\) | Massenfluss einer Komponente \(n_{i}=\rho_{i}u_{i}\) | \({\rm \frac{kg}{m^{2}\cdot s}}\) |
| \(N_{i}\) | Molarer Fluss einer Komponente; \(N_{i}=c_{i}u_{i}\) | \({\rm \frac{mol}{m^{2}\cdot s}}\) |
| \(J_{i}\) | Molarer Fluss relativ zu einem Beobachter, der sich im Bezugssystem der Geschwindigkeit \(U\) bewegt; \(J_{i} = c_{i} \cdot \left(u_{i}-U\right)\) | \({\rm \frac{mol}{m^{2}\cdot s}}\) |
| \(V_{A_{d}}\) | Relativgeschwindigkeit einer Komponente \(A\) bzgl. \(U\); \(V_{A_{D}} = u_{A} - U\) | \({\rm \frac{m}{s}}\) |
Für ein binäres System aus den beiden Komponenten \(A\) und \(B\) gilt: \[ U = \frac{1}{c} \left(c_{A}u_{A} + c_{B}u_{B}\right). \] und mit der in Tab. 1 gegebenen Definition der Größe \(N_{i}\): \[ U = \frac{1}{c} \left(N_{A} + N_{B}\right). \] Für den molaren Fluss \(J_{A}\) im Bezugssystems eines Beobachters, der sich mit der molaren Durchschnittsgeschwindigkeit bewegt, folgt: \[ J_{A} = N_{A } - \frac{c_{A}}{c} \left(c_{A}u_{A} + c_{B}u_{B}\right). \] Berücksichtigung von Gl. \ref{eqFick1} ergibt: \[ N_{A} = \frac{c_{A}}{c} \left(N_{A} + N_{B}\right) - D_{AB} \frac{\diff c_{A}}{\diff z}. \]
Diese Gleichung liefert den molaren Fluss \(N_{A}\) einer Komponente \(A\) in einer binären Mischung aus \(A\) und \(B\) bezüglich eines stationären Beobachters.
Der molare Fluss \(N_{A}\) besteht aus zwei Anteilen, dem Anteil \(\frac{c_{A}}{c} \left(N_{A} + N_{B}\right) \), der einem makroskopischen Fluss entspricht, und dem Anteil \( D_{AB} \frac{\diff c_{A}}{\diff z} \) , der diffusivem Stofftransport entspricht. Der Massentransport erfolgt gemäß dem 1. Fickschen Gesetz stets in Richtung abnehmender Konzentration.
Für Gase kann die Konzentration durch den jeweiligen Partialdruck ersetzt werden: \[ c_{A} = \frac{p_{A}}{RT}; \] und die Gesamtkonzentration an Spezies durch den Gesamtdruck: \[ c = \frac{P}{RT}. \] Damit nimmt der molare Fluss relativ zu einem stationären Beobachter folgende Form an: \begin{equation} \label{eqGasStrom1} N_{A} = \frac{p_{A}}{P} \left(N_{A} + N_{B})\right) - \frac{D_{AB}}{RT} \frac{\diff p_{A}}{\diff z}. \end{equation}Diffusion einer Komponente \(A\) durch eine stationäre Schicht einer Komponente \(B\) in der Gasphase.--
Wir betrachten eine Wasseroberfläche in Kontakt mit einer Strömung ungesättigter Luft. Wenn die Luft ungesättigt ist (relative Feuchte \(<100\%\)), werden Wassermoleküle in die Luftströmung hineindiffundieren. Wenn die Strömung laminar ist, wird die unterste Luftschicht stationär sein. Da für Luft (die Kompenente \(B\)) keine Nettodiffusion stattfindet, ist \(N_{B}=0\) und Gl. \ref{eqGasStrom1} nimmt folgende Form an:
\[ N_{A} = \frac{p_{A}}{P} \cdot N_{A} - \frac{D_{AB}}{RT} \cdot \frac{\diff p_{A}}{\diff z}. \] Dies lässt sich umstellen zu \[ N_{A} \diff{z} = - \frac{D_{AB}\cdot P}{RT\left(P-p_{A}\right)}. \] Unter stationären Bedingungen ist \(N_{A}\) eine Konstante (der Fluss ändert sich nicht mit der Zeit).Wir integrieren zwischen den Orten \(z=1\) und \(z=2\), also
\[ N_{A}\cdot \int_{z=1}^{z=2}{\diff z} = -\frac{D_{AB}P}{RT} \cdot \int_{p_{A_{1}}}^{p_{A_{2}}} \frac{\diff{p_{A}}}{P-p_{A}}. \]
Das Integral auf der linken Seite ist gleich \(N_{A}\cdot \left(z_{2}-z_{1}\right)\). Die rechte Seite ist elementar integrierbar [2]. Dividiert man beide Seiten durch \(z_{2} - z_{1}\), so erhält man als wichtiges Zwischenergebnis: \[ N_{A} = \frac{D_{AB}\cdot P}{RT \cdot \left(z_{2}-z_{1}\right)} \cdot \ln\frac{P-p_{A_{2}}}{P-p_{A_{1}}} \] Für das Stefanrohr können wir \(z_{2}-z_{1}\) gleich dem Abstand \(z\) zwischen dem Eintritt in das Strömungsrohr und dem Meniskus der Flüssigkeitsoberfläche setzen. Unmittelbar an der Flüssigkeitsoberfläche ist \(p_{A_{1}}=p^{D}\) (Dampfdruck von \(A\)), am Eintrittsort in das Strömungsrohr ist \(p_{A_{2}}=0\). Daher: \[ N_{A} = \frac{D_{AB}\cdot P}{RT \cdot z} \cdot \ln\frac{P}{P-p^{D}} \] Der Fluss \(N_{A}\) der Substanz \(A\) mit der Molmasse \(M_{A}\) hängt mit der Änderung \(\diff z\) des Flüssigkeitsspiegels beim Durchtritt durch die Fläche \(A\) zusammen: \[ \frac{A \cdot \rho_{A}}{M_{A}} {\diff z} = A \cdot N_{A} \cdot {\diff t} = \frac{D_{AB}\cdot P}{RT \cdot z} \cdot \ln\frac{P}{P-p^{D}} \cdot A \cdot {\diff t}. \] Wir schreiben vor dem Integrieren \(z\) auf die linke Seite: \[ \frac{A \cdot \rho_{A}}{M_{A}} z {\diff z} = A \cdot N_{A} \cdot {\diff t} = \frac{D_{AB}\cdot P}{RT } \cdot \ln\frac{P}{P-p^{D}} \cdot A \cdot {\diff t}. \] Wir integrieren über \(z\) bzw. über \(t\): \[ \frac{A \cdot \rho_{A}}{M_{A}} \cdot \frac{1}{2} \left(z_{2}^{2} - z_{1}^{2}\right) = \frac{D_{AB}\cdot P}{RT } \cdot \ln \frac{P}{P-p^{D}} \cdot A \cdot \Delta t. \]Beachten Sie bitte, dass \(z_{2}\) und \(z_{1}\) sich jeweils auf den Abstand des Meniskus zum Eintrittsort in das Strömungsrohr beziehen; die Differenz der Quadrate bezieht sich auf die Änderung des Abstandes zum Eintrittsort, also auf das Absinken des Flüssigkeits"-spiegels im Zeitintervall \(\Delta t\). Setzen wir die Zeit \(t\) zu Beginn der Messung (\(z=z_{1}\)) gleich Null, so können wir statt \(\Delta t\) auch einfach \(t\) schreiben.
An dieser Stelle erkennen wir, dass das Quadrat der Änderung des Flüsigkeitsspiegels mit der Zeit geht. Wir lösen wir nach \(D_{AB}\) auf und berücksichtigen die Identität \[ \ln\frac{P}{P-p^{D}} = - \ln 1-\frac{p^{D}}{P} \] sowie die Tatsache, dass \(A\) auf beiden Seiten der Gleichung steht; so gelangen wir zu \[ \frac{\rho_{A}}{2 M_{A}} \left(z_{2}^{2} - z_{1}^{2}\right) = - \frac{D_{AB}\cdot P}{RT } \cdot \ln \left(1-\frac{p^{D}}{P}\right) \cdot t. \] Wir isolieren nun \(D_{AB}\): \[ D_{AB} = - \frac{RT \rho_{A}}{2 M_{A} P } \cdot \frac{z_{2}^{2} - z_{1}^{2}}{t} \cdot \left[\ln \left(1-\frac{p^{D}}{P}\right)\right]^{-1}. \]Dies ist die Gl. \ref{eqStefan1}, wenn wir noch die auf der S. 3 gegebene Definition der Größe \(k\) anwenden und die hier verwendete Größe \(P\) durch \(p_{0}\) ersetzen (\(P\) ist in Lehrbüchern zum Massentransfer die übliche Bezeichnung für den Gesamtdruck).---