Hinweise zur Fehlerrechnung: Wir interessieren uns für den Fehler in \(\ln K\) und in \(\Delta H\), also für \(\Delta \ln K\) und \(\Delta \Delta H\).
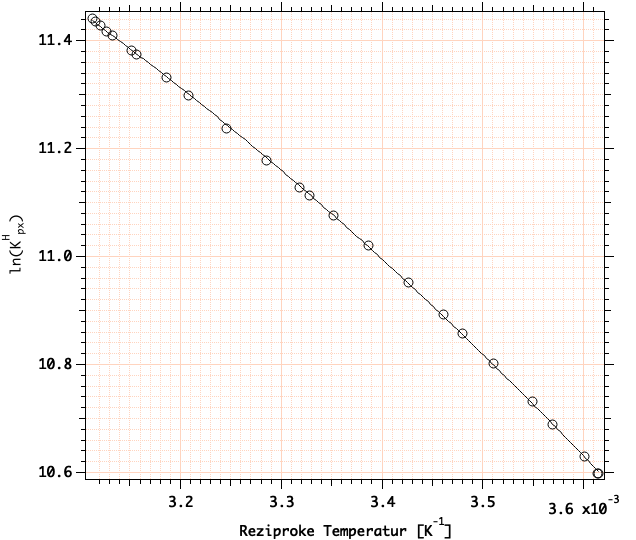
Die experimentell ermittelten \(\ln K\)-Werte streuen um die mathematische Ausgleichsfunktion \(\ref{eqBenson}\). Die zufälligen Messfehler sind die Ursache dieser Streuung. Als Folge sind die in Gl. \(\ref{eqBenson}\) auftretenden Koeffizienten \(a_{0}\) etc. mit einer Ungenauigkeit behaftet. Ihre Datenanalyse-Software gibt Ihnen diese Ungenauigkeit aus (meist als Standardabweichung \(\sigma\)). Damit können Sie für \(\ln K\) einen Fehler \(\Delta \ln K\) angeben. Gl. \(\ref{eqBenson}\) lautet (siehe weiter oben):
\begin{equation*}
\ln K^{H}_{px} = a_{0} + a_{1} \cdot \frac{1}{T} + a_{2} \cdot \left(\frac{1}{T}\right)^2.
\end{equation*}
Für den Fehler \(\Delta \ln K\) gilt dann:
\[
\Delta \ln K = \sqrt{
\left(\frac{\pdiff{\ln K}}{\pdiff a_{0}} \cdot \Delta a_0 \right)^2
+ \left(\frac{\pdiff{\ln K}}{\pdiff a_{1}} \cdot \Delta a_1 \right)^2
+ \left(\frac{\pdiff{\ln K}}{\pdiff a_{2}} \cdot \Delta a_2 \right)^2
} .
\]
Die partiellen Ableitungen müssen Sie selbst bilden (behandeln Sie hierzu die Koeffizienten \(a_i\) formal wie Variablen, nach denen Sie ableiten können; zum Beispiel ist \( \frac{\pdiff{\ln K}}{\pdiff a_{0}} = 1\) und \( \frac{\pdiff{\ln K}}{\pdiff a_{1}} = 1/T\)), die \(\Delta a_{i}\) liefert Ihnen die Analyse-Software. Ebenso kann der Fehler von \(\Delta H\) aus den Standardabweichungen der Koeffizienten berechnet werden:
\[
\Delta \Delta H = \sqrt{
\left(\frac{\pdiff{\Delta H}}{\pdiff a_{1}} \cdot \Delta a_1 \right)^2
+ \left(\frac{\pdiff{\Delta H}}{\pdiff a_{2}} \cdot \Delta a_2\right)^2
}.
\]
Eine systematische Analyse der Fehler der
Messgrößen ist also gar nicht notwendig.
Hinweise zum Logarithmieren: Zur Datenanalyse muss die Henry-Konstante logarithmiert werden. Wenn eine Größe, die \(n\) signifikante Stellen aufweist, logarithmiert wird, dann muss der Logarithmus der Größe nach dem Dezimalseparator (Punkt oder Komma) \(n\) Stellen aufweisen. Die Stellen vor dem Dezimalseparator entsprechen nur der Größenordnung des ursprünglichen Zahlenwertes und haben mit der Genauigkeit nichts zu tun.
Beispiel:
\(Z=1,723\) → \(\log Z = 0,2363\)
\(Z=17,23\) → \(\log Z = 1,2363\)
\(Z=172,3\) → \(\log Z = 2,2363\)
\(Z=1723\) → \(\log Z = 3,2363\)
Für den natürlichen Logarithmus (\(\ln\)) gilt dasselbe wie für den dekadischen Logarithmus (\(\log\)).