Physikalisch-Chemische Praktika

Aufgabenstellung

1. Aufnahme von Absorptionsspektren eines Indikatorfarbstoffes bei verschiedenen pH-Werten.
2. Bestimmung des isosbestischen Punktes der Absorptionsspektren und Normierung der Spektren auf den isosbestischen Punkt.
3. Bestimmung des Verhältnisses von protonierter und deprotonierter Form des Indikatorfarbstoffes bei den eingestellten pH-Werten.
4. Bestimmung der \({\rm pK_S}\)-Werte der Dissoziationsstufen des Indikatorfarbstoffes.

Grundlagen

1. In diesem Versuch soll die Lage eines Indikatorgleichgewichts spektroskopisch bestimmt werden. pH-Indikatoren spielen in der heutigen Laboratoriumspraxis eine weit weniger wichtige Rolle als in der Vergangenheit, weil moderne Redoxelektroden den pH-Wert eines wässrigen Systems auf drei (!) signifikante Stellen genau anzugeben vermögen. Zur spektroskopischen Quantifizierung eines chemischen Gleichgewichts stellen sie aber ein gutes Modellsystem dar.
   Aus der Allgemeinen Chemie ist bekannt, dass Indikatorfarbstoffe konjugierte Säure/Base-Paare im Sinne der Bronstedschen Säure/Base-Theorie darstellen. Häufig werden diese durch die Symbole HInd (protonierte Form) und \({\rm Ind^-}\) (deprotonierte Form) bezeichnet. Das Protolysegleichgewicht lautet dann: \begin{equation} \ce{HInd + H2O <=> H3O+ + Ind^-} \end{equation} Diese Schreibweise suggeriert, dass \(\ce{HInd}\) elektrisch neutral ist, während die deprotonierte Form als Anion vorliegt. Dies ist keinesweg immer der Fall; die protonierte Form kann auch ein (gegebenenfalls mehrfach geladenes) Kation sein; die deprotonierte Form wäre dann um eine Einheit weniger positiv geladen. Im übrigen kann der Indikatorfarbstoff auch mehrere abspaltbare Protonen, also mehrere Dissoziationsstufen aufweisen.

   Formal korrekt, aber sehr schwerfällig zu lesen, wäre die folgende Schreibweise für eine gegebene Dissoziationsstufe: \[ \ce{H_{n}Ind^{z+} + H2O <=> H3O+ + H_{n-1}Ind^{(z-1)+}} \]
2. Das chemische Gleichgewicht mit der Gleichgewichtskonstanten \(K_S\) (sogenannte Säurekonstante) ist gegeben zu: \begin{equation} \label{eqK_S} K_S = \frac{[\ce{Ind-}]}{[\ce{HInd}]} \cdot [\ce{H3O+}] \end{equation}
3. Das Konzentrationsverhältnis \(\frac{[{\rm Ind}^-]}{[{\rm HInd}]}\) eines Indikators ist wie folgt mit dem \({\rm pK_S}\)-Wert der Säure und dem vorliegenden pH-Wert verknüpft (Henderson-Hasselbalch-Gleichung, die logarithmierte und umgestellte Form von Gl. \(\ref{eqK_S}\)): \begin{equation} \label{eqHenderson} pH = pK_S + \log \frac{[{\rm Ind}^-]}{[{\rm HInd}]}. \end{equation} Diese Gleichung gilt auch für pH-Indikator-Farbstoffe. Da die Konzentration eines Indikator-Farbstoffes üblicherweise äußerst gering ist (\(c < 10^{-6}\;{\rm mol/L}\)), kann die Aktivität des Farbstoff-Anions mit seiner Konzentration gleichgesetzt werden.
   Das Verhältnis \(\frac{[{\rm Ind}^-]}{[{\rm HInd}]}\) ist für einen gegebenen pH-Wert eindeutig festgelegt. Ist beispielsweise der pH-Wert um eine Einheit kleiner als der \({\rm pK_S} \)-Wert des Indikators, so ist nach Gl. \(\ref{eqHenderson}\) \[ pH = pK_S - 1 = pK_S + \log \frac{[{\rm Ind}^-]}{[{\rm HInd}]} \] und daher \[ \log \frac{[{\rm Ind}^-]}{[{\rm HInd}]} = -1 \] und \[\frac{[{\rm Ind}^-]}{[{\rm HInd}]} = 10^{-1} = \frac{1}{10} = 10\%, \] so dass 90% des Indikators in der protonierten Form \(\ce{HInd}\) vorliegen. Ist der pH-Wert um eine Einheit größer als der \({\rm pK_S}\)-Wert, so liegen entsprechend 90% in Form der konjugierten Base vor. Bei einer Abweichung des pH-Wertes um 2 Einheiten vom \({\rm pK_S}\)-Wert liegen bereits 99% als Säure bzw. konjugierte Base vor. Beträgt der \({\rm pK_S}\)-Wert zum Beispiel \({\rm pK_S}=5\), dann liegt bei pH=3 die Säure praktisch undissoziiert und bei pH=7 fast vollständig dissoziiert vor. Dies ist in der Abb. 1 graphisch dargestellt.

   

4. Ist das Konzentrationsverhältnis \(\frac{[\ce{HInd}]}{[\ce{Ind-}]}\) aus Messungen bekannt, so kann durch Umstellen von Gl. \ref{eqHenderson} der \(pK_S\)-Wert des Säure/Base-Paares ermittelt werden: \begin{equation} \label{eqpKs} pK_S = pH + \log \frac{[\ce{HInd}]}{[\ce{Ind-}]}. \end{equation} Wird der pH-Wert durch Zugabe eines Puffers festgelegt, dann kann aus dem Verhältnis \(\frac{[\ce{HInd}]}{[\ce{Ind-}]} \) der \(pK_s\)-Wert erschlossen werden. Im vorliegenden Versuch wird dieses Verhältnis durch eine spektroskopische Messung bei verschiedenen pH-Werten ermittelt.
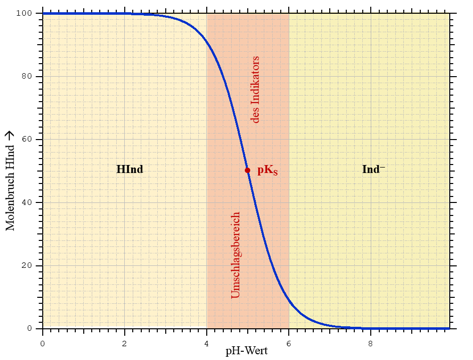
   Eine eingehende Diskussion von Indikatorfarbstoffen und ihrem quantitativen Verhalten ist in Referenz [2] zu finden.
5. Die protonierte und die deprotonierte Form eines Indikatorfarbstoffes unterscheiden sich in ihrem Lichtabsorptionsverhalten im sichtbaren Spektralbereich. Notwendige Grundlagen zur quantitativen Analyse von Photoabsorptionsprozessen können der Praktikumsskripte zum Versuch S11 entnommen werden. Hier wird nur das aus Lehrbüchern der Allgemeinen Chemie bekannte Lambert-Beersche Gesetz angeführt:[(1)] \begin {equation} \label{eqLB} \log \frac{I_0}{I} = \epsilon \cdot c \cdot d \end{equation} Hierin ist \(I_0\) gleich der Intensität der Strahlung nach dem Durchlaufen einer Küvette, die die Probe nicht enthält; \(I\) ist die Intensität nach dem Durchlaufen der probehaltigen Küvette. Der Ausdruck \(\log \frac{I_0}{I}\) auf der linken Seite von Gl. \ref{eqLB} wird Extinktion genannt und mit \(E\) bezeichnet; er ist dimensionslos. \(\epsilon\) ist der molare dekadische Extinktionskoeffizient, der üblicherweise in der Einheit \(\frac{\rm L}{\rm mol \cdot cm}\) angegeben wird. Er ist eine stoffspezifische Größe und hängt von der Anregungswellenlänge ab.
   Es ist wichtig, zwischen der Extinktion \(E\) auf der linken Seite von Gl. \(\ref{eqLB}\) und dem molaren dekadischen Extinktionskoeffizienten \(\epsilon\) auf der rechten Seite von Gl. \(\ref{eqLB}\) genau zu unterscheiden. Löst man Gl. \(\ref{eqLB}\) nach \(\epsilon\) auf, so erhält man \(\epsilon = \frac{E}{c\cdot d}\). Der Extinktionskoeffizient \(\epsilon\) ist also die auf die Konzentration und Schichtdicke normierte Extinktion.
6. Isobestischer Punkt: Nehmen wir an, bei einem chemischen Prozess gehe die Substanz \(\ce{HInd}\) (unser Indikatorfarbstoff) in die Substanz \(\ce{Ind-}\) über, so dass sich ein Gleichgewicht zwischen beiden einstellt (bei den in diesem Versuch untersuchten Indikatorgleichgewichten ist dies zum Beispiel der Fall): \[ \ce{Hind <=> Ind-}. \]
   Wir betrachten die Abb. 2; diese zeigt schematisch das Photoabsorptionsspektrum (\(\epsilon\) als Funktion der Wellenlänge) der reinen Substanz \(\ce{HInd}\) (rotes Spektrum). Das Spektrum der reinen Substanz \(\ce{Ind-}\) ist in blauer Farbe eingetragen. Die beiden Spektren schneiden sich bei \(\lambda = 600\;{\rm nm}\). Dieser Schnittpunkt wird isosbestischer Punkt genannt, die entsprechende Wellenlänge bezeichnen wir mit \(\lambda_{\rm iso}\). Hier sind die Extinktionskoeffizienten beider Substanzen einander gleich. Den entsprechenden Extinktionskoeffizienten nennen wir \(\epsilon_{\rm iso}\). Es gilt also \(\epsilon_{\ce{HInd}} = \epsilon_{\ce{Ind-}} = \epsilon_{\rm iso}\) für \(\lambda = \lambda_{\rm iso}\).

   

   \(\ce{HInd}\) liege ursprünglich mit der Konzentration \([\ce{HInd}]=c^0\) vor. Dann ist für beliebige Lage des Gleichgewichtes: \([\ce{Ind-}] = c^0 - [\ce{HInd}]\).

   Für eine beliebige Wellenlänge gilt bezüglich der Extinktion \(E\): \[E_{\ce{HInd}} = \epsilon_{\ce{HInd}} \cdot [\ce{HInd}] \cdot d\] und \[E_{\ce{Ind-}} = \epsilon_{\ce{Ind-}} \cdot [c^0 - [\ce{HInd}] \cdot d\]

   Enthält die Küvette den reinen Stoff \(\ce{HInd}\) ohne Beimischung von \(\ce{Ind-}\) in der Konzentration \([\ce{HInd}]=c^0\), so ist die Extinktion am isosbestischen Punkt gleich \[ E_{\ce{HInd}} = \epsilon_{\rm iso} \cdot c^0 \cdot d \] und falls der reine Stoff \(\ce{Ind-}\) in derselben Konzentration \(c^0\) enthalten ist, \(\ce{HInd}\) aber abwesend ist (weil sich \(\ce{HInd}\) vollständig in \(\ce{Ind-}\) umgesetzt hat), gilt für die Extinktion durch \(\ce{Ind-}\): \[ E_{\ce{Ind-}} = \epsilon_{\rm iso} \cdot c^0 \cdot d \] mit demselben \(\epsilon=\epsilon_{\rm iso}\).
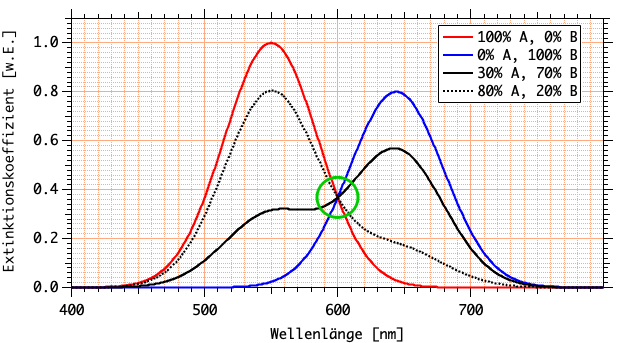
   Demnach ist am isosbestischen Punkt nicht nur der Extinktionskoeffizient \(\epsilon\), sondern auch die Extinktion \(E\) beider Substanzen gleich, wenn sie in Abwesenheit der anderen in derselben Konzentration \(c^0\) vorliegen: \[\left(E_{\ce{HInd}} = E_{\ce{Ind-}}\right)_{\lambda = \lambda_{\rm iso}} .\]
   Liegt \(\ce{HInd}\) ursprünglich in der Konzentration \(c^0\) vor, und geht \(\ce{Ind-}\) aus \(\ce{HInd}\) hervor, und sind die aktuellen Konzentrationen gleich \([\ce{HInd}]\) und \([\ce{Ind-}]\), dann gilt für die Gesamtextinktion \(E_{\Sigma}\) bei der Wellenlänge \(\lambda=\lambda_{\rm iso}\): \begin{align*} E_{\Sigma} &= E_A + E_B \\ &= \left[\epsilon_{\rm iso} \cdot [\ce{HInd}] \cdot d\right] + \left[\epsilon_{\rm iso} \cdot [\ce{Ind-}] \cdot d \right]\\ &= \left[\epsilon_{\rm iso} \cdot [\ce{HInd}] \cdot d\right] + \left[\epsilon_{\rm iso} \cdot (c^0 - [\ce{HInd}]) \cdot d \right]\\ &= \epsilon_{\rm iso} \cdot [\ce{HInd}] \cdot d + \epsilon_{\rm iso} \cdot c^0 \cdot d - \epsilon_{\rm iso} \cdot [\ce{HInd}] \cdot d\\ &= \epsilon_{\rm iso} \cdot c^0 \cdot d. \end{align*}

   Hieraus folgt die für die Analyse der Messdaten fundamentale Tatsache:

   Eine beliebige Mischung aus \(\ce{HInd}\) und \(\ce{Ind-}\) wird am isosbestischen Punkt \(\lambda = \lambda_{\rm iso}\) dieselbe Extinktion \(E = E_{\rm iso}\) aufweisen wie \(\ce{HInd}\) und \(\ce{Ind-}\) mit der Konzentration \(c^0\) allein, solange nur insgesamt \([\ce{HInd}] + [\ce{Ind-}] = c^0\).

7. Normierung auf den isosbestischen Punkt. Wegen experimentell unvermeidlicher Streuungen in der Konzentration des Indikatorfarbstoffes werden sich die einzelnen, experimentell ermittelten \(\log \frac{I_0}{I}\)-Kurven nicht von vorneherein im isosbestischen Punkt schneiden.
   Wir müssen daher die experimentell ermittelten Absorptionsspektren der Gemische erst geeignet normieren, nachdem aus den Grenzspektren der reinen Substanzen A und B der isosbestische Punkt ermittelt worden ist.

   Dies erfolgt in den folgenden Teilschritten:

   1. Subtraktion einer Konstante vom experimentell ermittelten Spektrum des Gemischs, so dass die langwellige Asymptote eine Extinktion von Null aufweist (die Substanz absorbiert dort nicht).
   2. Nachfolgende Multiplikation mit einem Faktor, so dass sich das Spektrum im isosbestischen Punkt mit den Spektren der Grenzfälle A und B schneidet.

   Damit machen wir uns von eventuellen Abweichungen in der Gesamtkonzentration unabhängig. Als Fehler verbleibt aber eine eventuelle Ungleichheit in der Konzentration der Grenzfälle und damit eine Genauigkeitsschranke für \(\lambda_{\rm iso}\).
   Erst die Normierung auf den isosbestischen Punkt erlaubt den Vergleich der Spektren!
   
8. Durch Linearkombination der beiden Grenzspekten und Vergleich mit dem gemessenen Spekrum eines Gemisches kann der relative Anteil beider ermittelt werden, wenn eine Normierung auf den isosbestischen Punkt vorgenommen wurde. Dies kann man von Hand durch Ausprobieren ermitteln, oder eine Datenanalyse-Software heranziehen. Eine genau Herleitung ist hier verlinkt. Für jede Wellenlänge des Absorptionsspektrums eines Gemisches aus \(\ce{HInd}\) und \(\ce{Ind-}\) gilt für die Gesamtextinktion \(E\) des Gemisches beider Substanzen, falls die eine aus der andreren hervorgegangen ist: \begin{equation} \label{eqk1k2} E = k_{\ce{HInd}} \cdot E_{\ce{HInd}} + k_{\ce{Ind-}} \cdot E_{\ce{Ind-}} \end{equation} mit der Randbedingung \(k_{\ce{HInd}} + k_{\ce{Ind-}} = 1\). Das Verhältnis \(\frac{k_{\ce{HInd}}}{k_{\ce{Ind-}}}\) stellt das Konzentrationsverhältnis der Substanzen \(\ce{HInd}\) und \(\ce{Ind-}\) in der Gleichgewichtsmischung dar.

   Gl. \ref{eqk1k2} ist zusammen mit Gl. \ref{eqpKs} die Grundlage zur Auswertung der Messdaten und zur Bestimmung des \(pK_S\)-Wertes des untersuchten Indikatorsystems.

Durchführung

1. Wägen Sie ungefähr 25 mg des Indikatorfarbstoffes Thymolblau ab, notieren Sie die genaue abgewogene Menge, überführen Sie die abgewogene Menge in einen 50-mL-Messkolben und füllen Sie mit Ethanol bis zum Eichstrich auf.
2. Überführen Sie mit einer Pipette^[1] 0,5 mL der hergestellten Lösung in ein Becherglas und fügen Sie mit einer Pipette 19,5 mL Pufferlösung pH=9 hinzu. Füllen Sie eine Quarz-Küvette^[2] mit der Lösung und stellen Sie diese in den Probenraum des Spektrometers (vordere Halterung, »Probe«).
3. Stellen Sie eine mit Pufferlösung gefüllte Küvette ohne Farbstoff in den hinteren Schacht im Probenraum (»Referenz«).
4. Nehmen Sie das Absorptionsspektrum im Modus %T^[2] im gesamten zugänglichen Wellenlängenbereich (200 nm < λ < 900 nm) auf und speichern Sie als Text-Datei ab. Dieses Spektrum nennen wir das Probespektrum.
5. Füllen Sie die Probenküvette mit der Ethanol/Pufferlösung ohne Indikatorfarbstoff und in demselben Konzentrationsverhältnis Ethanol/Puffer und verankern Sie die Küvette im Probe-Strahlengang. Die Referenzküvette bleibt im Referenzstrahl. Nehmen Sie das %T-Spektrum auf und speichern Sie es als Textdatei ab. Dieses Spektrum nennen wir das Referenzspektrum.
6. Lesen Sie beide Spektren in eine Datananalyse-Software (Beispiel: IGOR PRO) ein. Teilen Sie das Referenzspektrum durch das Probespektrum und logarithmieren Sie das Resultat dekadisch. Sie erhalten auf diese Weise die Extinktion der Probe im Bereich 200 nm < λ < 900 nm.
7. Nehmen Sie Spektren bei den pH-Werten 0, 1, 2, 3, 6, 8, 9 und 12 auf (jeweils wie oben gezeigt herstellen!). Stellen Sie jeweils die Extinktion \(E\) als Funktion der Wellenlänge graphisch dar.
8. Stellen Sie für den pH-Bereich 6-12 die Spektren in derselben Abbildung graphisch dar, bestimmen Sie aus den Spektren mit pH=6 und pH=12 die Wellenlänge des isosbestischen Punktes und normierten Sie die Spektren mit pH=8 und 9 in der oben angegebenen Weise auf den isosbestischen Punkt.
9. Wiederholen Sie diese Vorgehensweise fur den pH-Bereich 0–6.

Auswertung

1. Lesen Sie die Spektren in das Programm ein.
2. Normieren Sie die Spektren auf den gemeinsamen isosbestischen Punkt.
3. Ermitteln Sie entsprechend Gl. \ref{eqk1k2} die relativen Beiträge der Grenzfälle zum Spektrum eines Gemisches.
4. Bestimmen Sie hieraus gemäß Gl. \ref{eqpKs} den \(pK_S\)-Wert des Indikatorsystems.
5. Vergleichen Sie Ihr Ergebnis mit Literaturdaten. (2)

Literatur

[1] Die Pipette wird senkrecht an die schräg gehaltene Wandung des beabsichtigten Aufnahmegefäß gehalten und die Flüssigkeit abgelassen. Hierbei beträgt die Wartezeit nach Ablassen der Flüssigkeit ca. 15 Sekunden. Am Ende wird die Pipette wieder an der Glaswand abgestreift. Da die Pipette auf Auslauf geeicht ist, ist der in der Spitze verbliebene Flüssigkeitsrest nach Ablauf bei der Eichung berücksichtigt worden. NICHT ausblasen!! ↩

[2] Die Küvetten weisen zwei mattierte und zwei transparente Flächen auf. Die transparenten Flächen müssen in den Strahlengang gestellt werden.↩

[3] Unter %T ist das Verhältnis \(\frac{I}{I_0}\) zu verstehen. Diese Größe ist nicht logarithmiert!↩